
[Contents] [Chapter I] [Chapter II] [Chapter III] [Chapter IV]
(I only briefly list some interesting properties without proofs and generalizations; some day this part may be expanded. If you have any solutions to problems raised here or know about other interesting properties of the game and boards, please let me know.)
Let us investigate the figures of pieces of one player on an empty board.
The figure of the four pieces of a player in which they are in the starting position on the Mentuldesk is called the doma. As the doma can freely move across the board (regaining its shape at every second or third move), it does not matter where it is located on the board:

The concept can easily be generalized to locally Euclidean boards (with square squares) of any dimension (the number of pieces in the doma would then be 2^dim), and maybe to several other boards with well-defined starting positions, too.
A figure of pieces is called domatizable if it can be transformed into a doma by a sequence of legal moves. The following picture shows an example of a domatizable figure. It can be domatized for instance by these four moves: 1. e3-e4-e5 2. f6-e5-d4 3. d7-e5-f3 4. f3-e4-d5.

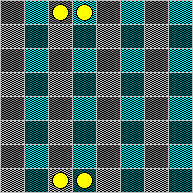
Not all the figures of pieces on the Mentuldesk are domatizable:

It is easily seen that the two pairs of pieces in the above picture are 'locked' in their files and cannot come closer to each other than three squares. Clearly no indomatizable position can occur in a real play (except maybe for some obscure boards with a non-symmetrical symmetry relation).
The domatizability of a figure depends on the board used. The following picture shows a figure which is clearly indomatizable on the Mentuldesk; on the torus, however, it is a doma.
For each of the locally Euclidean boards (of any dimension) there is an interesting question as to how many (and which) figures are domatizable. The problem is easily soluble by using a computer and I leave it to the reader, but some trivial observations can be made at once.
First, let us exclude some trivial cases. If the board can be colored in a similar way as the Mentuldesk so that every piece is bound to its starting color, then clearly no position with wrongly 'colored' pieces can be domatized. On such boards, let us consider only the 'color conforming' positions.
Similarly, no statura of four pieces can be domatized (since there are no legal moves at all). On some boards (e.g. the torus), however, there are no statura positions of four pieces at all. The question how many (color-conforming) statura positions are possible on a particular board is an interesting problem itself (the necessary condition being of course the totality ratio less than 1).
If the board has a non-trivial group of symmetry (most boards have), positions identical except for a symmetry of the board may be considered as identical. Furthermore, we can take as identical any two positions that can be transformed into each other by a sequence of legal moves (we thus factorize the set of all positions by the equivalence of mutual transformability). Then we will have the only domatizable figure (up to the transformability equivalence)---the doma. However, the number (and a classification) of equivalence classes of the factorization is a non-trivial problem (any statura, for example, has its own equivalence class).
Other interesting problems are these:
The following table shows how many squares of a board can at best be reached with a given number of pieces. The critical number of pieces (see Loss of Pieces) is pointed out with red color.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | More | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Mentuldesk, Cylinder 8*8, Torus 8*8 |
1 | 8 | 48 | 64 | |||||||
| Moebius 8*8 | 1 | 16 | 64 | 64 | |||||||
| 3D 8*8*8, 3-Torus 8^3 |
1 | 8 | 48 | 256 | 320 | 384 | 448 | 512 | |||
| 120-cell | 1 | 10 | 30 | 120 | 120 | ||||||
| 4-Torus 3^4 | 1 | 3 | 9 | 27 | 81 | 81 |
The critical number of pieces, if it exists, may be used as a definition of the 'Mentula-dimension' of the board.
The table shows the percentage of the square pairs that have their target square defined, i.e. they do not aim off the board. This can serve as a measure for the totality of the symmetry function or, in other words, the absence of borders in the particular board. Boards with no borders have the number equal to 1; the less the number, the more borders abound in the board. On boards with totality ratio 1 there are usually no statura positions of two or more pieces.
The ratio, however, has only a relative expressing power, since the number may be very low on the boards of higher dimensions although there is room enough for making moves. The total number of squares and the dimension of the board play also an important role, and so the percentage only provides meaningful comparison for boards of the same class (e.g. 3D locally Euclidean boards 8x8x8).
For the game importance of this characteristics see Figures of Pieces.
| Totality Ratio | Squares | Dimension | |
|---|---|---|---|
| Mentuldesk | 0.25 | 64 | 2 |
| Cylinder, Moebius | 0.5 | 64 | 2 |
| Torus, Klein, Projective | 1 | 64 | 2 |
| n-dimensional Cube m^n | 1/2^n | m^n | n |
| n-dimensional p-Cylinder m^n | 1/2^(n-p) | m^n | n |
| n-dimensional Torus m^n | 1 | m^n | n |
| 120-cell | 1 | 120 | 3 |
Note: The ratio is slightly different if the pairs that cannot be used for moves are excluded. These are the pairs (a,a) for all boards and such pairs that S(a,b) = a or S(a,b) = b. The Mentuldesk has then the 'effective border ratio' 15/63 = 0.238095... instead of 16/64 = 0.25 etc.
The torus 3^4 can also be viewed as the four-dimensional vector space over the field Z_3 of integers modulo 3, or as a (two-dimensional) affine plane over the field (Z_3)^2. In the latter case the lines of the affine plane contain nine, not three points each; but of these, only three are accessible for a couple of pieces located on the line, using the common definition of the symmetry function on finite affine planes. Effectively (in Mentula sense) therefore the affine plane over (Z_3)^2 is equivalent to the 4D vector space over Z_3, and in this (four-dimensional) sense we will speak of subspaces etc.
Let us call a one-dimensional subspace of the board the line, a two-dimensional one the plane and a three-dimensional one the hyperplane. The squares of the board may also be called points in this section and the board denoted by (Z_3)^4. Points lying in the same line will be called colinear, those in the same plane coplanar and those in the same hyperplane cospatial.
There are 81 points, 1080 lines, 1170 planes and 120 hyperplanes in the whole board; 27 points, 117 lines and 39 planes in each hyperplane; 9 points and 12 lines in each plane; and 3 points in each line. In a plane, each point coincides with 4 lines. In a hyperplane, each point coincides with 13 lines and 13 planes and each line is included in 4 planes. In the whole (Z_3)^4, each point coincides with 40 lines, 130 planes and 40 hyperplanes, each line is included in 13 planes and 13 hyperplanes and each plane in 4 hyperplanes.
Every square neighbors with any other (by a corner at least). Since the (cyclic) lines contain only three squares each, a player's piece can only be captured if an adversary's pieces occupy the two remaining squares of any line it is located on. A couple of pieces aim at the same square no matter which one of them jumps over the other. When (and only when) there are three pieces at a line, they defend each other.
The only possible statura position is of three pieces located at the same line (or nine pieces filling a two-dimensional subspace, twenty-seven pieces in a hyperplane and, of course, the whole board either filled with pieces or empty). Unlike the Mentuldesk, in (Z_3)^4 the statura positions may be temporary, since an adversary capturing a piece would 'unblock' the player (however, since the pieces in statura defend each other, it is usually unwise to capture a piece in statura, even when the statured player is the last adversary on the board, unless the attacking player has all six pieces---else he gets locked in a smaller subspace and loses more points than the statured player).
Every non-cospatial figure of a player's pieces can be transformed to any other non-cospatial figure of the same number of pieces (excluding the statura position here of course). The same is true for every cospatial non-coplanar and every coplanar non-colinear figures.
[Contents] [Chapter I] [Chapter II] [Chapter III] [Chapter IV]