[Contents] [Chapter I] [Chapter II] [Chapter III] [Chapter IV]
Since Mentula has just one simple rule for moves, it is quite easy to modify the game replacing the Mentuldesk by another board of a different size, shape and/or geometric properties. Various kinds of such boards will be described in this chapter.
The only reference to the board in the motion rule is that to the 'symmetrical position' of the target square. This 'symmetry' is in fact a relation between three squares: the starting one, where the moving piece originally stood, the middle one, where the pivot piece stands, and the target one, where the moving piece stands after making its move. Therefore, any non-empty set with an arbitrary ternar relation defined on it can pricipially serve as a board for Mentula game. (Elements of the set forming the board will always be called 'squares', even though they may have a totally different shape or no shape at all.)
There are, however, some extra requirements that make a board more suitable for playing Mentula (for instance, a board consisting of just one square is plainly useless). A reasonable size of the board and balanced completness of the symmetry relation are those indispensable ones (if the symmetry relation were complete, just any move would be possible and the game would lose any sense; if it were empty, no moves would be possible at all and all players would be in statura). It is helpful if the symmetry relation can naturally be recognized from the structure of the board (for instance, if it is a real symmetry of the squares); it is preferable if the symmetry relation is a function, i.e. if there is at most one target square for every pair of the starting and middle squares, as it makes the game more similar to that with the standard Mentuldesk. It is even more preferable if the symmetry function S is symmetrical (i.e. if it holds for any squares a, b, c that S(a,b) = c implies S(c,b) = a), as it corresponds to the symmetry of the relation on the standard board. All the boards described further in this chapter will satisfy these reasonable conditions.
The symmetry function, however, need not be total: it is not true even with the standard Mentuldesk. If the symmetry function is total, the board can be regarded as one 'with no borders'.
For every board, the number of players, the number of pieces and the starting position are to be set. Often these data follow naturally from the structure of the board; otherwise the number of players and pieces should be set adequate to the size of the board and the starting position rule may be evaded by introducing the rule that the players will place their pieces to the squares of their choice in the first moves of the game.
Roughly said, you get a locally Euclidean board if you glue together zero or more pairs of opposite sides of the common Mentuldesk. Of course, there is no need to glue them physically (in some cases it would even be impossible in the 3D space); you just make the moves as if they were glued. The matter is a redefinition of the symmetry function, which in the case of locally Euclidean boards is quite simple and can readily be perceived without any complex calculation. In this subchapter we discuss the two-dimensional locally Euclidean boards only; those of higher dimensions are mentioned in the subchapter on multi-dimensional boards.
Good web pages about two-dimensional locally Euclidean spaces are these:
There are several locally Euclidean Mentula boards, listed below.
The Mentuldesk falls within the class of locally Euclidean boards, too: it is the Mentuldesk with zero pairs of its sides glued.
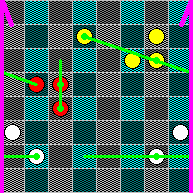
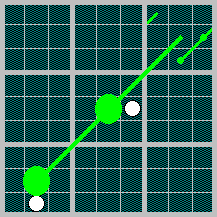
If you glue one pair of the opposite sides of a Mentuldesk to each other in the straightforward way, you get a board topologically equivalent to the cylinder. The magenta lines in the following picture indicate the sides that are identified (and their orientation---on the cylinder, they form an arrow). The green lines show examples of possible moves: 1. b2-g2-d2 d7-g6xb5 c4-c5-c6.

Please note that on the non-standard locally Euclidean boards the shifted starting position must be used, since in the standard starting position the players are able to capture an adversary's pieces at the first move.
If you glue together both pairs of opposite sides of the Mentuldesk in the straightforward way, you get a board topologically equivalent to the torus. Again the sides to be identified are indicated by magenta arrows, green lines show examples of possible moves: 1. d3-c8-b5 f2-h3-b4 e4-h7-c2.

As with the cylinder, you glue just one pair of opposite sides, but reverse the orientation of the identified sides by twisting the board first, so that the square a1 is adjacent to h8, a2 to h7 etc. The following picture shows the Moebius board and the way moves across the glued line are performed. The magenta lines indicate the sides that are identified and the orientation of glueing (they form an arrow on the strip). The green line shows a possible move of White.
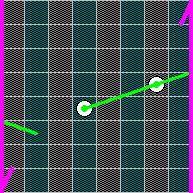
You may notice that the Moebius board (as well as the Klein bottle) is not colored with four colors as the Mentuldesk, since the pieces do not preserve the Mentuldesk colors of their squares. They only preserve the parity of the file they are placed on; the board is therefore two-colored.
Similarly, a cylinder with an odd number of files can only be colored with two colors for ranks. The situation with other locally Euclidean boards of different sizes is a simple exercise and I omit the discussion here.
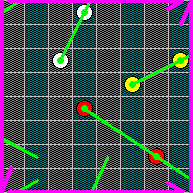
You identify two opposite sides preserving the orientation (as with the cylinder) and the other pair reverting the orientation (as with the Moebius strip). This cannot be done in the three-dimensional space (only in the four-dimensional one), but the board can still exist and is topologically equivalent to the Klein bottle. The following picture shows examples of possible moves on the Klein bottle: 1. c6-d8-e2 (both horizontal sides are glued straightforward, the move looks like on the torus) f5-h6-b2 (going through the vertical sides reverts the direction of the line on the diagram; on the Klein bottle the line is straight) d4-g2-b1 (the line goes through h1, a8 and a1 to b1).
If you glue both pairs of opposite sides reversely (not possible in 3D space either), you get a board topologically equivalent to the projective plane. Technically it is not a locally Euclidean board (since the point corresponding to the lower left and upper right corners has only two adjacent squares a1 and h8, and similarly the point corresponding to the other two corners), but since the properties of the board are much the same as of locally Euclidean boards, we place it here. The following diagram shows examples of possible moves on the projective plane: 1. e6-d8-f2 g5-h6-a2 e4-g2-h1.
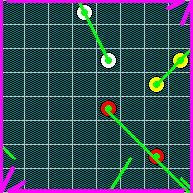
The projective plane cannot be colored in any way, because every piece can get to any square of the board.
It is possible to play Mentula on a three-dimensional Mentuldesk---in the cube 8*8*8. The position of pieces in the cube can conveniently be given on a two-dimensional paper by cutting the cube into horizontal layers of its cubic squares; these layers are effectively two-dimensional and can be diagrammed beside each other in a row. Moves are then calculated as shown in the following picture: first find the layer at which the pair of pieces aims, then imagine the starting and pivot pieces located in the target layer and calculate the destination square as usually. If we denote the layers by A, B, C, ... and the squares in the layers by common algebraic notation, then the green lines show the calculation of the move Db1-Cc1-Bd1 in the cube 4*4*4 (the smaller size of the board used for simplicity):

In the cube, each player may have eight pieces and the squares are colored with eight colors. There are symmetrical starting positions for four and eight players (two-player game is too boring).
The four-dimensional Mentuldesk can be diagrammed the same way: the three-dimensional layers (being the rows of two-dimensional diagrams) are put below each other, so that they form a two-dimensional array of two-dimensional diagrams. The moves are calculated the same way as with three-dimensional board: the target two-dimensional diagram (in which the destination will be calculated in the common way from the projections of both pieces) is in this array calculated as if the diagrams were atomic squares.
This way we can continue to any higher dimension, making a hierarchy of two-dimensional diagrams of diagrams of diagrams of squares. In higher dimensions these diagrams get a bit large; but there is always an option of blindfold play.
As with two-dimensional boards, it is possible to glue one or more pairs of opposite sides of the (hyper)cube and get the multi-dimensional analogues of the two-dimensional cylinder. Let us call the n-dimensional cube with p sides glued the (p of n)-cylinder and the (n of n)-cylinder the n-dimensional torus or n-torus. By twisting the board in a higher dimension and flipping the sides before gluing them one can obtain multi-dimensional locally Euclidean boards; their diagramming would be as usual.
As an example of multi-dimensional torus boards, let us describe the four-dimensional torus of 3*3*3*3 squares. As explained above, it can be diagrammed as an array of 3*3 diagrams of 3*3 squares. The picture shows how moves are calculated according to the method described above.
There is probably no good symmetrical starting position for players' pieces, so the rule of placing the pieces to the squares of the player's choice in the first moves must be adopted. Each player should have six pieces, since five is the least number of pieces not bound to a subspace and one should be a spare as with the Mentuldesk.
For further information about the board, see the section about its mathematical and game properties.
Surfaces of Platonic polyhedra consist of regularly distributed cells which would be ideal for playing Mentula, defining the symmetry function in the obvious way along the surface. Unfortunately, the tetrahedron, the cube and the octahedron are (apart from other disqualities) too small for any meaningful play and the dodecahedron and the icosahedron do not conform to the condition required of the symmetry function: if we start at a cell and go 'straight' through a neighboring cell the same distance on, we get to an edge, not another cell. Fortunately though, there is a polytope in the fourth dimension, the regular 120-cell, which is large enough and which does conform to the condition on the symmetry function and so Mentula can be played on its surface.
There are many web pages dedicated to the 120-cell; I am therefore going to describe it only briefly and direct the reader for further information, e.g., to the Wikipedia article on the 120-cell.
The cells of the 120-cell are regular dodecahedra. Like the dodecahedron or icosahedron in the three-dimensional space, the 120-cell resembles a (four-dimensional) sphere (a football of a sort). If we take any of its surface dodecahedra as a pole, then there is an opposite dodecahedron as the other pole; between them, the dodecahedra are arranged in a sort of 'layers' (like the parallels of latitude on a sphere), which themselves resemble three-dimensional hollow balls composed of dodecahedra. The first layer consists of the twelve dodecahedra adjacent to the pole dodecahedron, then there are twelve others adjacent to their opposite faces and twenty more filling the 'holes' between these two layers. At their farther faces, the latter twelve neighbor with their counterparts on the other hemisphere, but between these two dozens, at the level of their common faces, filling the space between them there are thirty others, having the same distance from both of the poles and forming the 'equator' of the polytope. Going on we get the symmetrical layers of twelve, twenty and twelve on the opposite hemisphere, arriving at last to the second pole.
If someone starts at the pole and goes ever 'straight ahead', leaving each dodecahedron at the face opposite to that through which he entered, he gets to the other pole at the fifth step and back to the starting pole at the tenth step, having circled the whole 120-cell in a closed line of dodecahedra. (Note however, that though these ten dodecahedra form a 'great circle' across the polytope, they do not divide it into two hemispheres, since we are one dimension higher.)
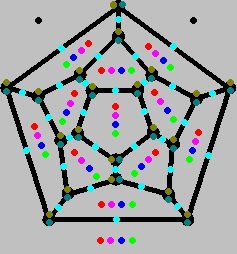
The way in which the dodecahedra are placed on the surface of the 120-cell enables a graphical representation of Mentula positions in a two-dimensional diagram: the four layers consisting of twelve dodecahedra have their elements located 'right above' the faces of the pole dodecahedron (in the same sense as for instance Australia is located 'above' a corresponding place on the South Polar Circle), the dodecahedra of the two layers of twenty are located above the vertices of the pole dodecahedron and the equatorial dodecahedra are high above the edges of the pole dodecahedron. Mentula can therefore be played on the vertices, edges and faces of the planar graph of the dodecahedron (with two more squares for the poles), marking the layer in which the piece is located by some extra means. The moves, however, cannot be calculated easily from such a diagram (except for trivial cases like both pieces in the equator etc.) and so one must learn to visualize the 120-cell and use the diagram only to record a position. The following picture shows an example of a diagram for the 120-cell.
The fact that the equatorial dodecahedra of the regular 120-cell correspond to the edges of the pole dodecahedron implies that Mentula can also be played on the edges of regular dodecahedron (and in fact on the edges of any Platonic polyhedron). Since three-dimensional polyhedra can be viewed as tessellations of the two-dimensional sphere, it leads to the idea that Mentula could be played on edges of any regular tessellation of the two-dimensional sphere or plane or hyperbolical plane. Indeed, on any regular planar graph (finite or an aptly chosen part of an infinite one) allows playing Mentula as described below.
When calculating a move, we find a way from the starting edge to the pivot piece, remembering the order and direction of the turns we had to make. Then we proceed from the pivot piece making the same turns but reverting their order and direction. It does not matter which way from the starting piece to the pivot one we choose.
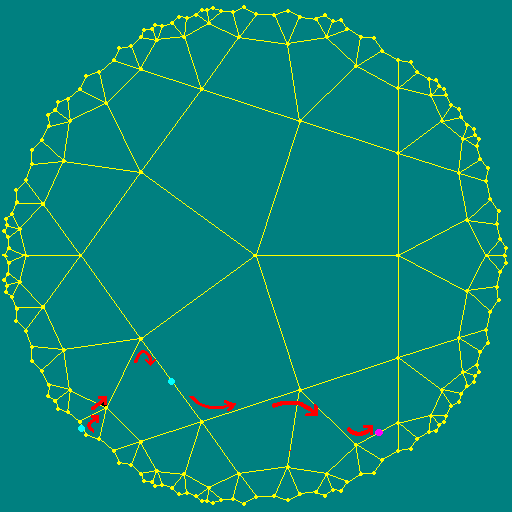
An example should make it clear: let us take a part of the regular {4,5}-tessellation of the hyperbolical plane for our board. The move on the picture is calculated as follows: arriving to the pivot piece we first turned right, then we took the second left, and finally right; so we proceed left (corresponds to the final right), then the second right and finish with the left turn (for the first right turn).
When searching for other boards, one may get the following ideas:
Regular polytopes of higher dimensions. However, in any dimension higher than four the only regular polytopes that exist are the simplex, the hypercube and the dual to the hypercube. The simplices and the hypercube duals have a wrong arrangement of the cells for the symmetry relation. The hypercubes of higher dimensions do have enough cells for playing Mentula, but their geometry make the game uninteresting: any piece that can move aims at the opposite cell no matter where the other pieces are. Maybe edges (or hyperedges) of some higher-dimensional polytopes could make a Mentula board; if you prove (or disprove) this hypothesis, please let me know.
Affine planes. However, finite affine planes have the same symmetry relations as the two-dimensional tori, so they bring nothing new.
Tilings of the plane or of a higher-dimensional space (taking the tiles, not the edges for squares). However, the regular tilings of the plane have the symmetry relation isomorphic to that of the common square Mentuldesk. Those of other tilings with regular polygons I checked were either isomorphic to the square mentuldesk or there were no natural symmetry relation definable on them. But still there may exist a tiling in a Euclidean or hyperbolical space of a dimension greater than one that is good for playing Mentula. I will be grateful if anyone who discovers any such tiling will send me a note.
There may also exist good boards based on another principle than those mentioned here. If you have an idea, please do inform me.
[Contents] [Chapter I] [Chapter II] [Chapter III] [Chapter IV]